1 时空图

事件 ⚓

物理总是抽象出模型：质点、点电荷、直导线、平面波……运动学一般研究质点的运动——位置随时间的变化。然而不久我们就会发现，我们好像连位置、时间都不清楚怎么描述，于是只好先退一步，研究“事件”。

“渐近故乡时，冷风吹进船舱中，呜呜的响”就是一事件。正如乒乓球作为质点时不管是橙是白，这里也不在意事件具体发生了什么（“冷风吹进”，“呜呜的响”），而主要关心它发生的时刻（“渐近故乡时”）和位置（船舱）。用数学的冷眼看，它的时空坐标只是 $ (x, t) $ 这样一个有序数对／向量／点。

注意，我们所说的事件是瞬时局部的点。“看鸟雀来吃时，我远远地将缚在棒上的绳子只一拉，那鸟雀就罩在竹匾下了。”这就不是一个事件，而是三个。也可以想见，描述质点的运动需要一系列事件，而非一个。

时空图 ⚓

总之，位置$x$、时刻$t$是一个事件的关键属性，我们可以在“$ Oxt$ 平面”内用点表示它。时空图基本就是指这种“$x$-$t$图”。

类似地，质点的运动在“$ Oxt$ 平面”内用线表示，称作世界线。（质点的任意运动都可表示为线，那么所有的线都存在对应的运动吗？）

时空图：闰土·鸟雀·竹匾

稍微思考一下，我们至少能从时空图中读出以下信息：

任意时刻物体的位置。
两个事件是否同时或同地，以及时间间隔（时间差）、空间间隔（距离）。
物体是否相对参照系静止，以及运动速度。

刚才那个时空图中的空间只有一维；二维空间的时空图类似一沓_儿照片摞在一起；实际上狭义相对论的背景空间是 $(\vec x, t)$ 所在的 $\R^4$，或者写成 $ \R^{3+1} $。

0.06 sec — 原子弹爆炸¹的时空图，某种“锥”（向上代表时间流逝，向纵深、左右和一个照片无法体现的方向代表空间延伸，领会精神:-）

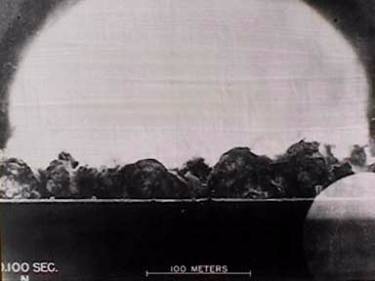
0.016 sec — 原子弹爆炸¹的时空图，某种“锥”（向上代表时间流逝，向纵深、左右和一个照片无法体现的方向代表空间延伸，领会精神:-）

例：冰盘碰冰车 ⚓

张三、李四各自坐在冰车上相向而滑，他们约定谁先用鞋或手杖碰冰面谁就算输。然而张三了解宇宙飞船怎样减速，于是提前载了冰盘，预备到时推出，让冰盘带着动量直奔李四。这样自己能主动均匀变速，而李四则面临与冰盘硬碰硬，甚至还可能滑下冰车。

假设李四不作任何防备，冰盘与他的冰车发生瞬时完全弹性正碰。张三希望回收冰盘（冰盘碰撞后能追上他），那么需要满足什么条件？相关物理量请自行设出。

分析 ⚓

冰盘碰冰车（不按比例在扭曲的空间绘制——随便画的）

分析整个过程，得到上图。（以李四（点线）滑下冰车（实线）为例）

临界时，冰盘碰撞后与张三共速，恰好追不上他。换句话说，黄线（冰盘）第二段与紫线（张三）第二段平行。
事件
- “推出”前后动量守恒，总动能增加（具体增加多少取决于张三），且与李四无关。~~另外如果推得太轻，冰盘有可能追不上李四。~~
- “碰撞”前后动量守恒，能量（总动能）守恒，且与张三无关。另外由于碰撞时间很短，而李四坐冰车的压力有上界，故他们之间摩擦的冲量可忽略，因此起作用的质量只包括李四的冰车。
- “回收”前后动量守恒；不过临界时这个点在无穷远，我们不关心。
整个过程前后动量守恒，（如果能“回收”）冰盘在此是细节，不用考虑；总动能似乎可增可减。临界时末态张三、冰盘共速，考虑动能、动量时相当于已经回收了。

计算 ⚓

分别记张三（和冰车）、李四（的冰车）、冰盘作 $3,4,0$；分别记初态（initial）、末态（final）作 $i,f$，具体所指视语境。

“推出”：
\[(m_3+m_0) v_{3,i} = m_3 v_{3,f} + m_0 v_{0,f}.\]
“碰撞”：

动量：$ m_0 v_{0,i} + m_4 v_{4,i} = m_0 v_{0,f} + m_4 v_{4,f} $。

能量：$ \frac12 m_0 {v_{0,i}}^2 + \frac12 m_4 {v_{4,i}}^2 = \frac12 m_0 {v_{0,f}}^2 + \frac12 m_4 {v_{4,f}}^2 $。

可以解得（记得）
\[v_{0,i} + v_{0,f} = 2 \frac {m_0 v_{0,i} + m_4 v_{4,i}} {m_0 + m_4},\]

另：关于 $v_0, v_4$ 的方程组 $p_0 + p_4 = p \land E_{0} + E_{4} = E $ 有两组根，那么就对应 $i,f$。消去$v_4$，得 $ m_0 m_4 {v_0}^2 + \left( p - m_0 v_0 \right)^2 = 2 m_4 E $。其中二次项 $ {v_0}^2 $ 的系数是 $ m_0 \left( m_0 + m_4 \right) $，一次项 $v_0$ 的系数是 $ -2p m_0 $，于是两根和 $ v_{0,i} + v_{0,f} = 2 p / \left( m_0 + m_4 \right) $。
临界条件：$v_{3, \text{推出} f} = v_{0, \text{碰撞}f}$。

另外 $ v_{0, \text{推出} f} = v_{0, \text{碰撞}i} $。

综合三式，整理成关于 $ v_{0, \text{推出} f}, v_{3, \text{推出}f } $ 的线性方程组。（其中 $i$ 指整个过程的初态）

\[\begin{bmatrix} m_0 & m_3 \\ m_4 - m_0 & m_4 + m_0 \end{bmatrix},\, \begin{bmatrix} p_{30, i} \\ 2 p_{4, i} \end{bmatrix}\]

然后可以解出来一长串_儿，具体就不算了……(⊙_⊙)

注意“能回收”本应是 $ v_{3, \text{推出} f} \ {\color{red} \geq}\ v_{0, \text{碰撞}f} $，所以第二行实际是“$\geq$”。“相向而滑”又保证了 $ p_{4,i} < 0 < p_{30,i} $。因此，临界条件无解（$ m_0 \left( m_3+m_4+m_0 \right) = m_3 m_4$）对应总能回收。

一些讨论 ⚓

在这个问题中，动量守恒等价于质心速度不变（用线段长给定质量比，则质心位置可用尺规作出）。在“碰撞”附近，能量（总动能）守恒（在动量守恒的基础上）等价于“下图中的四边形是平行四边形”。

从图判断能量（总动能）是否守恒（$ m_A : m_B = 2:1 $）

作图步骤

垂直于 $t$ 轴随意作一直线，分别交两条世界线于两点。
以碰撞点为中心，作上述直线的对称直线，又与两条世界线交出两点。
连接这四点。

原因

作图其实是选取了三个时刻（垂直于 $t$ 轴的直线上的每个事件同时发生）：碰撞前、碰撞、碰撞后。这三个时刻等距，划分出两段等长时间（碰撞前~碰撞，碰撞~碰撞后），从而位移正比于速度。

以 A（橙色）为例，这条世界线交出的两点的 $x$ 坐标差正比于（两段时间的）速度的和，即 $ v_i + v_f $。

而前面已经说明，无论是哪一方，都有 $ v_i + v_f = 2 v_c $，其中 $v_c$ 是质心速度。因此双方的 $ v_i + v_f $ 一样，所以这组对边平行。（另一组自不必说）

另：也可从“相对速度反向”理解。

运用这些性质，可用尺规补全下图，还能求出张三、冰盘、李四的质量比（用线段长之比表示）。

是否显示构造
点线连接而成，虚线平行而得。张三、冰盘、李四的质量比为 $2:1:3$。

冰盘碰冰车（被用白色墨水弄脏的残图）

图片取自Estimate of the energy released in the first Atomic Bomb explosion。这是个“抄本”，它指出原文在一个已经坏掉的链接。 ↩